鐵人賽Day 19- 使用Turf.js進行空間資料內插

web
  1. 1. 前言
  2. 2. IDW(inverse distance weighting)
  3. 3. TIN(Triangulated Irregular Network)
  4. 4. Voronoi Diagram
  5. 5. 後記

前言

今天的主題是空間資料內插(interpolation)，內插是GIS很重要的課題，因為我們拿到的資料(例如觀測站資料)很常是point，內插可以幫助我們把這些離散的資料變成面狀成果，這樣除了方便資料視覺化，也可以進一步進行空間分析。

本文是參加鐵人賽的文章，同步發表於 “2018鐵人賽-30天打造我的WebGIS系列”

內插有很多演算法，我們今天使用turf.js，在client端也可以做即時的內插運算，今天就試著來說明：

  • IDW法(規則網格)
  • TIN(不規則三角網)
  • Voronoi Diagram

在開始之前，先補充說明，GIS內插方法在GIS已相當成熟，GIS軟體如ArcGIS、QGIS、GRASS…等等強大老牌的工具都有更進階的方法(Bilinear, Kriging, nearest neighbor)且較多參數可調整的工具可以使用，turf.js是讓我們可以簡單在前端使用^^。

IDW(inverse distance weighting)

IDW法概念很簡單，每個內插點(網格)的值與鄰近樣本點的關係是距離，距離越遠關係越小。所以取值點與樣本點間的距離為權重進行加權平均，離內插點越近的樣本點賦予的權重越大。

已知其坐標和值為Xi，Yi, Zi （i=1,2,3,4,5..）距離加權值求(Xp,Yp)點值，每個則Zp值以下公式。（gisgeography）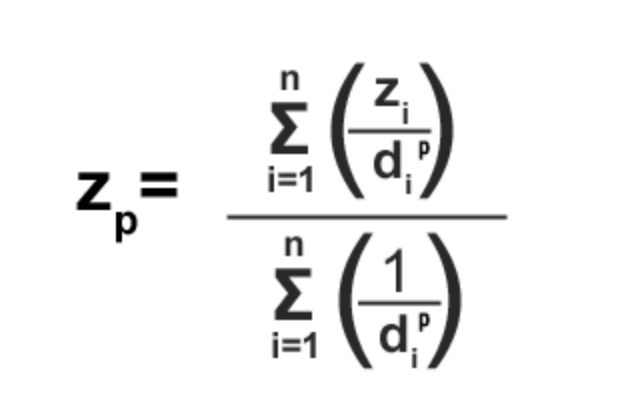

跟昨天一樣，以randomPoint產生隨機點的點作為示範，並隨機給定一個觀測值obs：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//產生隨機點
var ramdompts_ipl = turf.randomPoint(25, { bbox: [121.41, 24.34, 121.8, 24.65] });
turf.featureEach(ramdompts_ipl, function (point) {
  point.properties.obs = Math.random() * 20;
});
ramdomLayer_ipl.addData(ramdompts_ipl).addTo(map);
map.fitBounds(ramdomLayer_ipl.getBounds());


//放入圖層
var ramdomLayer_ipl = L.geoJson(null, {
  pointToLayer: function (feature, latlng) {
    return L.marker(latlng, {
      icon: L.icon({
        iconUrl: "./dist/assets/img/icon-black.png",
        iconSize: [12, 12],
        iconAnchor: [0, 6]
      }),
    }).bindPopup(feature.properties.obs.toFixed(3).toString());
  }
});

在turf.js中，interpolate這個方法就是IDW法：

1
2
var idw_grid = turf.interpolate(ramdompts_ipl, 2, { gridType: 'hex', property: 'obs', units: 'kilometers' });
//成果會是geojson

interpolate有幾個參數，包含內插點的間距(2)、內插得值(obs)、間距的單位(kilometers)、以及gridType(turfjs)。

特別說明一下ㄓgridType，目前有’square’ | ‘point’ | ‘hex’ | ‘triangle’ 可以選，例如本範例是用hex，輸出的成果就會是蜂巢狀的hexgrid。
除此之外，我們可能會使用square或triangle，因此這個方法是在規則的形狀中，計算內插值，只是格子不一定是方形的。

加入圖層，並給定色階：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
var idw_gridLayer = L.geoJson(idw_grid, {
  onEachFeature: function (feature, layer) {
    layer.bindPopup(feature.properties.obs.toFixed(3).toString());
  },
  style: function (feature) {
    return {
      "color": getColor(feature.properties.obs),
      "opacity": 1,
    }
  }
}
).addTo(map);

//色階
function getColor(x) {
  return x < 5 ? '#bd0026' :
    x < 10 ? '#f03b20' :
      x < 15 ? '#fd8d3c' :
        x < 20 ? '#fecc5c' :
          '#ffffb2';
};

成果：
square

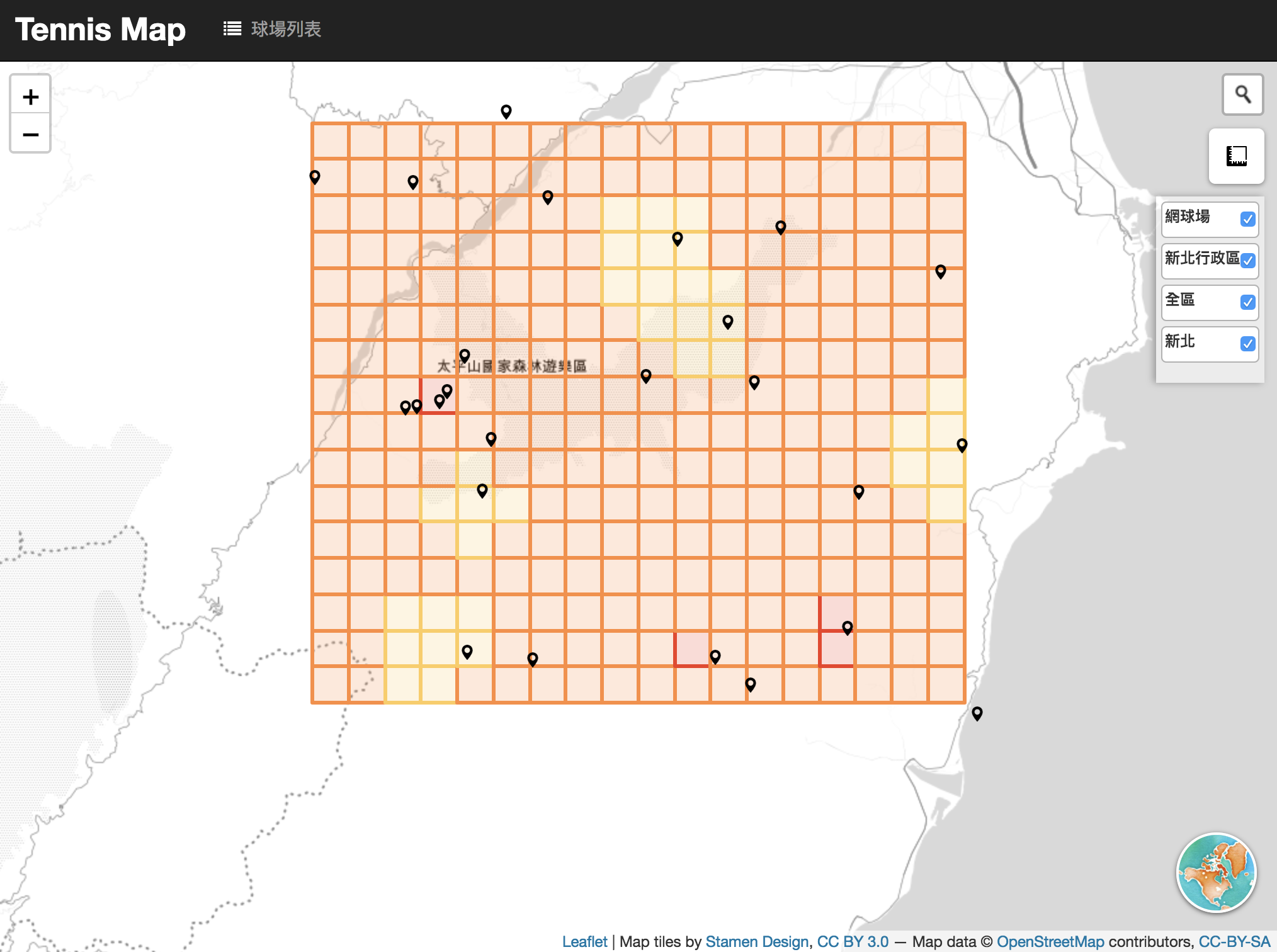
hex grid

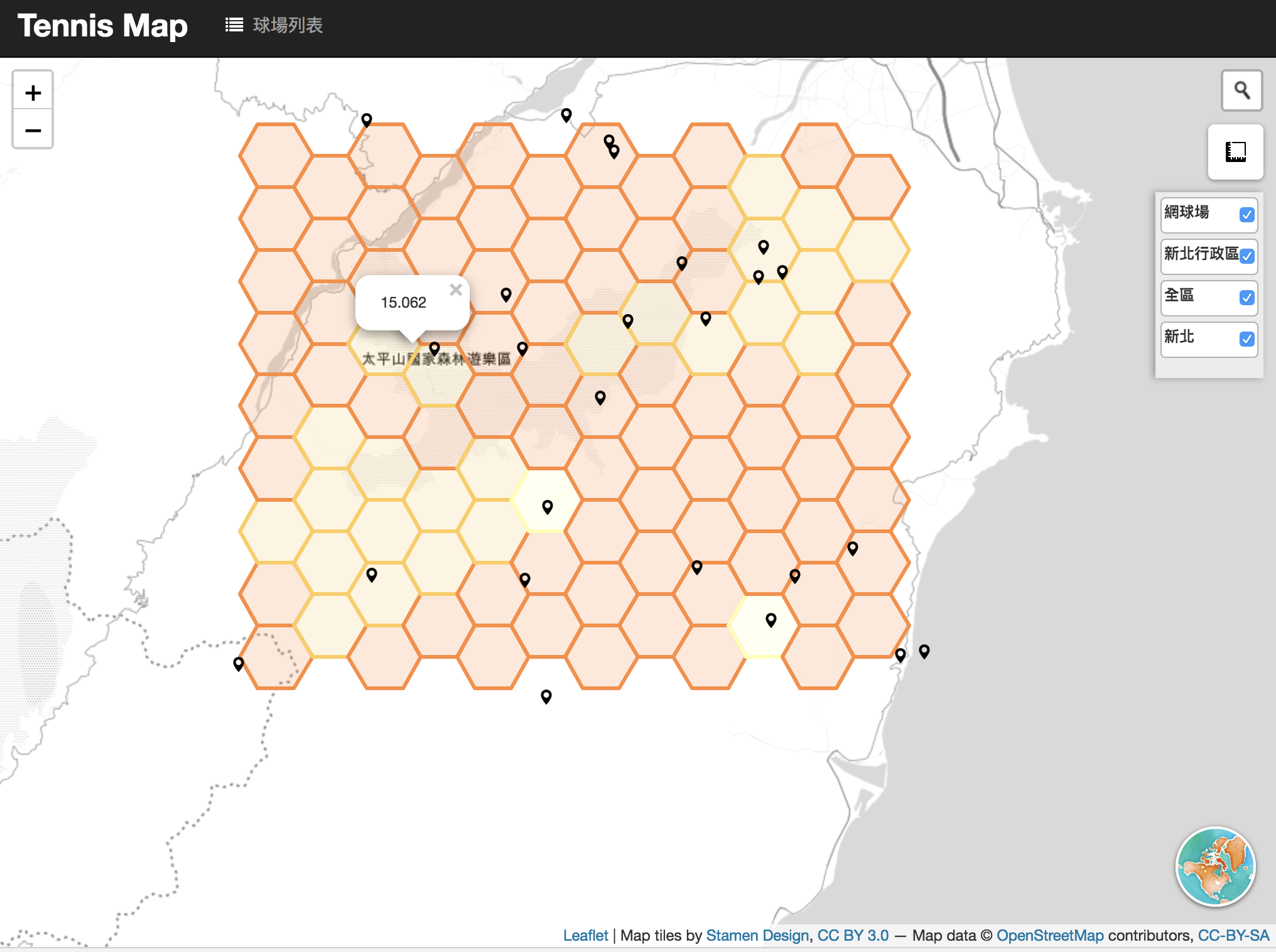
TIN(Triangulated Irregular Network)

TIN是不規則三角網，在電腦視覺領域或是GIS都很常見，跟前面IDW法是內插在規則的形狀中有所不同，TIN組成的不規則三角網是將樣本點連成連續的三角網，而在眾多產生三角網的演算法中，Delaunay三角化是公認最佳解：

Delaunay三網化：資料中任三點取其外接圓，若此圓內沒有包含任何其它點，則這三角形加入三角網中。這樣的目的是讓三角形都能越接近正三角形，狹長得三角形出現機會越低，因為三角形三邊長若越接近，外接圓越小。
(wiki)

在turf中，產生TIN的方法也很簡單：

1
2
//把前面的隨機點拿來用用
var tin = turf.tin(ramdompts_ipl, 'obs');

加入圖層：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//放到圖層中
var tinLayer = L.geoJson(tin, {
  onEachFeature: function (feature, layer) {
    var obs = feature.properties.a + feature.properties.b + feature.properties.c;
    feature.properties.obs = obs / 3;
    layer.bindPopup(feature.properties.obs.toFixed(3).toString());
  },
  style: function (feature) {
    var obs = feature.properties.a + feature.properties.b + feature.properties.c;

    return {
      "fillColor": getColor(obs),
      "weight": 0.5,
      "color": '#bd0026',
      "opacity": 1,
    }
  }
}
).addTo(map);

其中，設定的obs為三角網三頂點要記錄的東西，每個三角形分別會記錄到a,b,c三個頂點，要進行內插，我們就組好TIN之後把三角形內的頂點取平均作為三角形的值囉。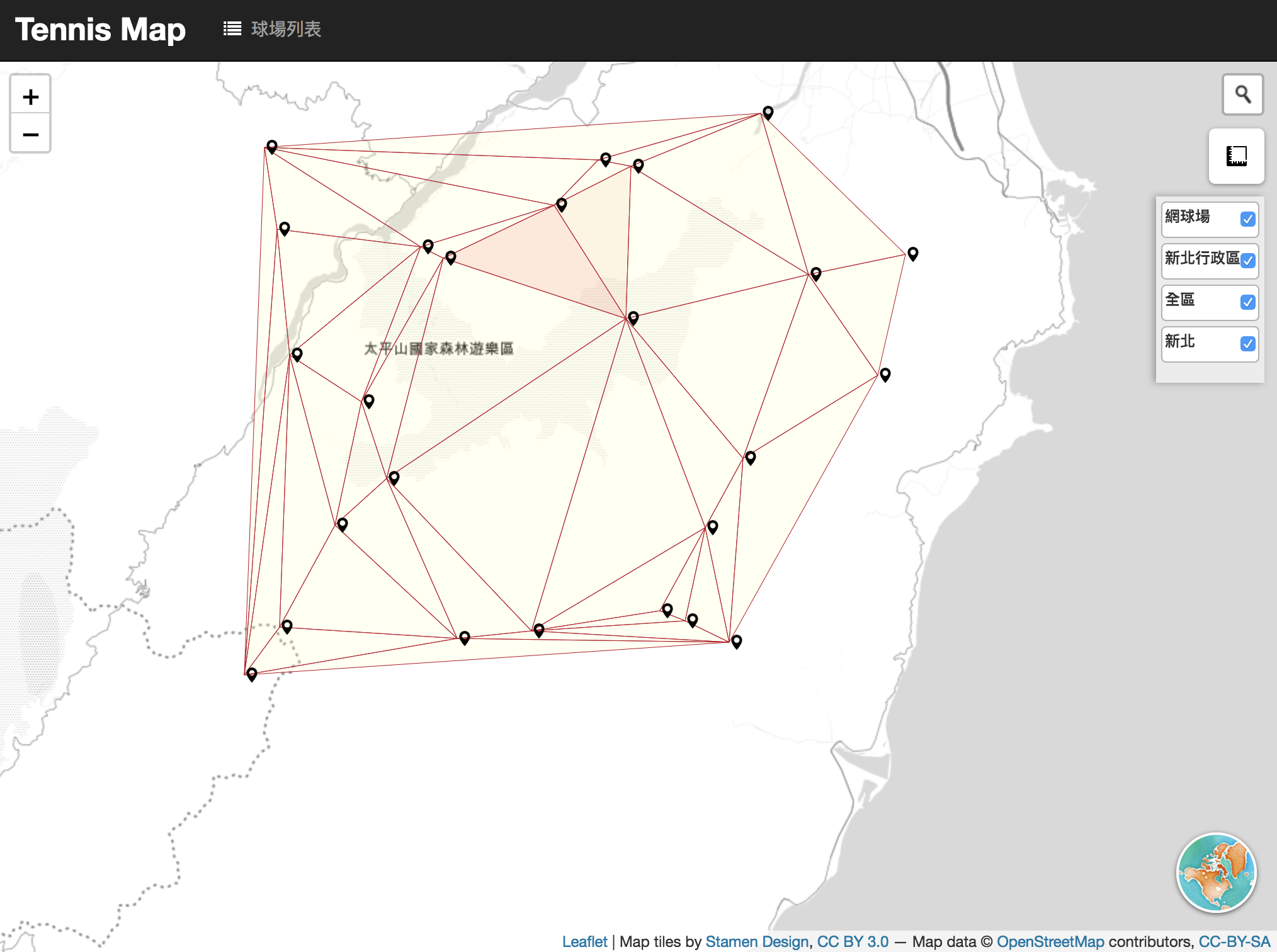

比較一下前面的成果，跟用interpolate把gridType設為triangle

1
2
var idw_grid = turf.interpolate(ramdompts_ipl, 2, 
{ gridType: 'triangle', property: 'obs', units: 'kilometers' });


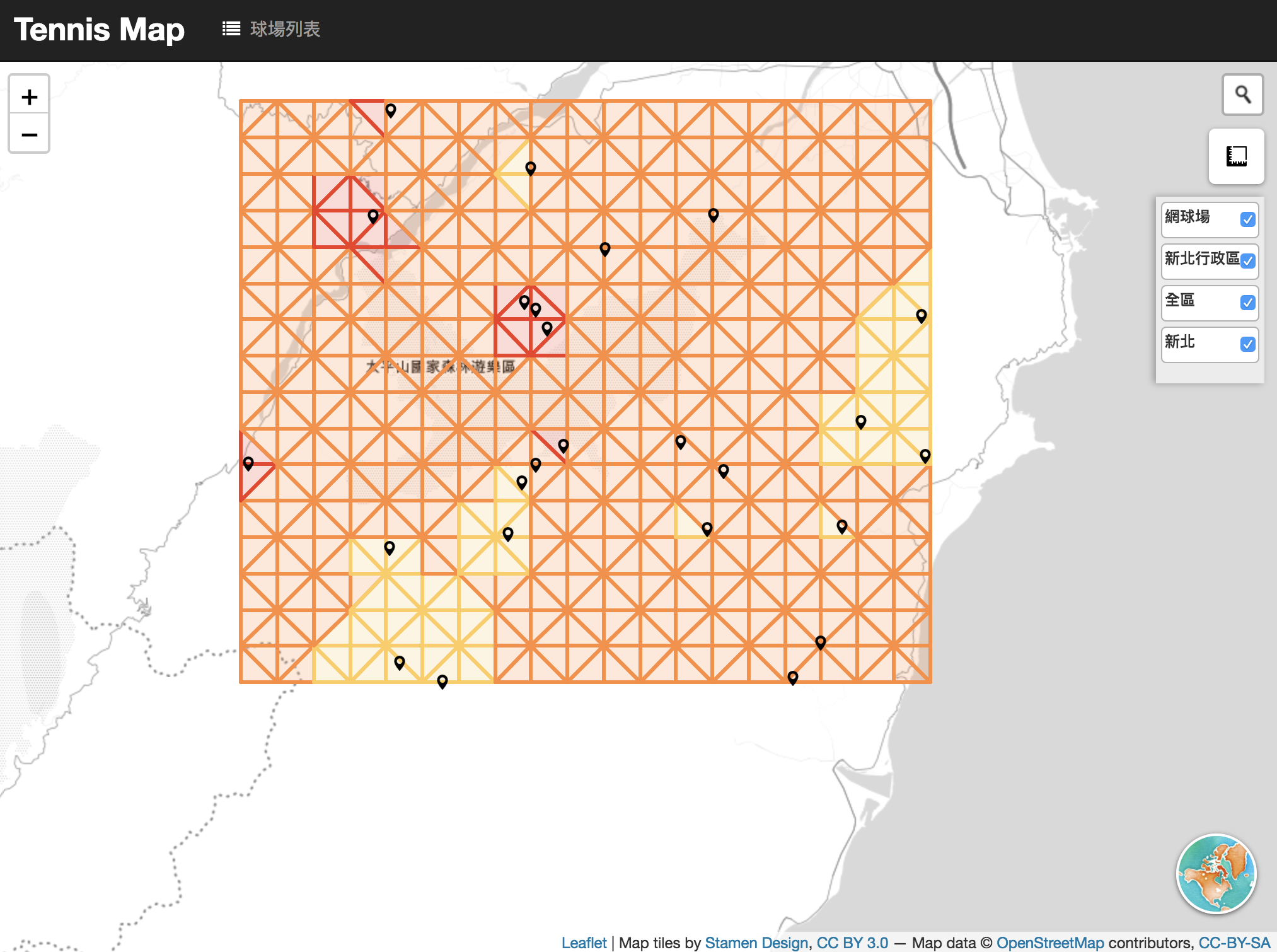
感覺TIN省很多圖形～

Voronoi Diagram

前面TIN講到Delaunay，那就一定要再提到Voronoi Diagram，兩者是對偶關係：

Voronoi Diagram：鄰近的點的中垂線，形成 Voronoi Diagram。(演算法筆記)

Voronoi Diagram 能表達的是最近或範圍的概念，在地理學上非常適合哪來將點的資料轉成面資料。

turf.js產生Voronoi Diagram的方法：

1
2
var voronoiPolygons = turf.voronoi(ramdompts_ipl,
  { bbox: [121.41, 24.34, 121.8, 24.65] });

在每個Diagram中塞入值：

1
2
3
turf.featureEach(voronoiPolygons, function (feature, index) {
  feature.properties.obs = ramdompts_ipl.features[index].properties.obs;
});

加入圖層：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var voronoiLayer = L.geoJson(voronoiPolygons, {
  onEachFeature: function (feature, layer) {

    layer.bindPopup(feature.properties.obs.toFixed(3).toString());
  },
  style: function (feature) {

    return {
      "fillColor": getColor(feature.properties.obs),
      "weight": 0.5,
      "color": '#bd0026',
      "opacity": 1,
    }
  }
}
).addTo(map);

成果：
Voronoi Diagram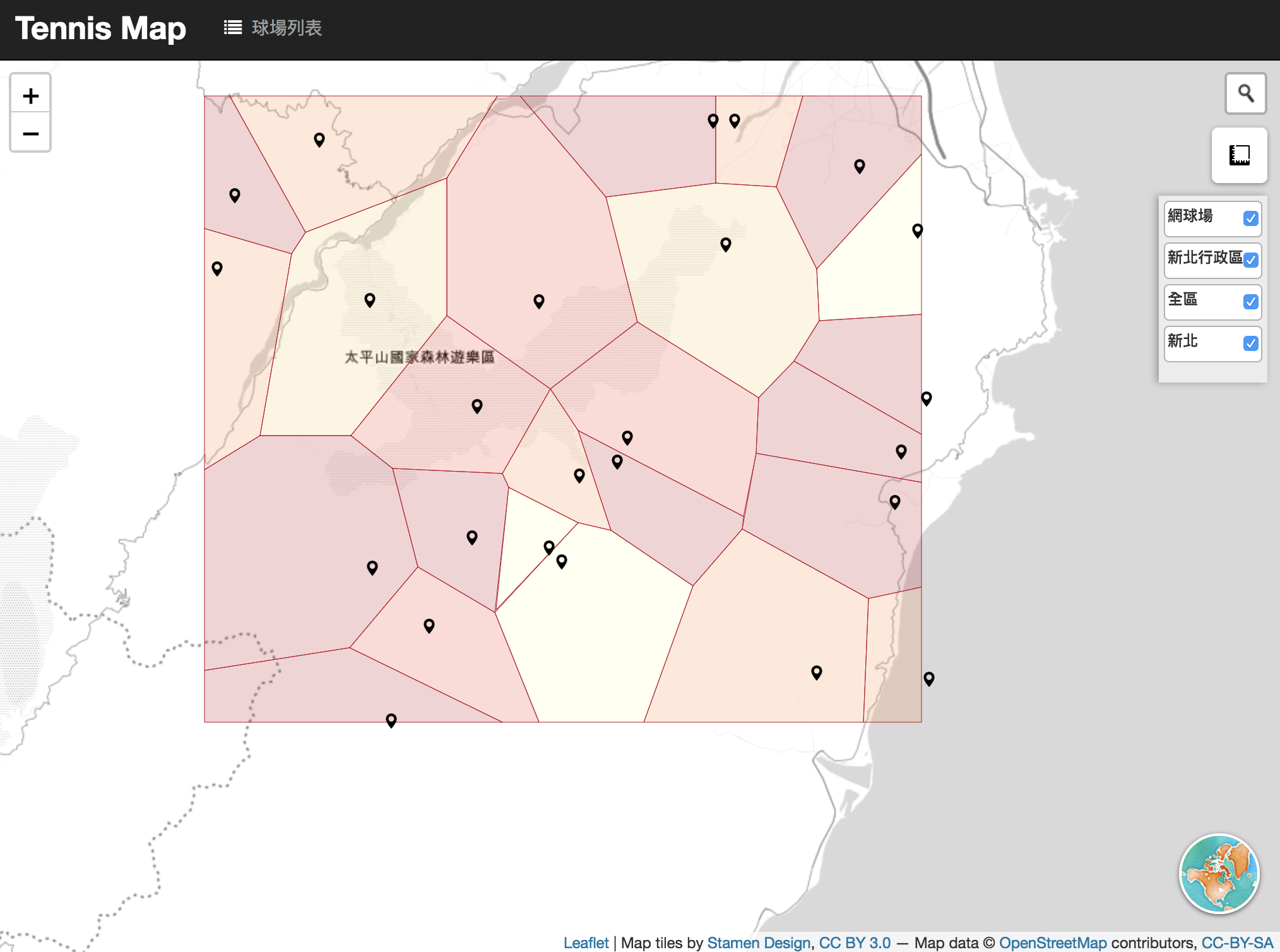

套疊TIN與Voronoi Diagram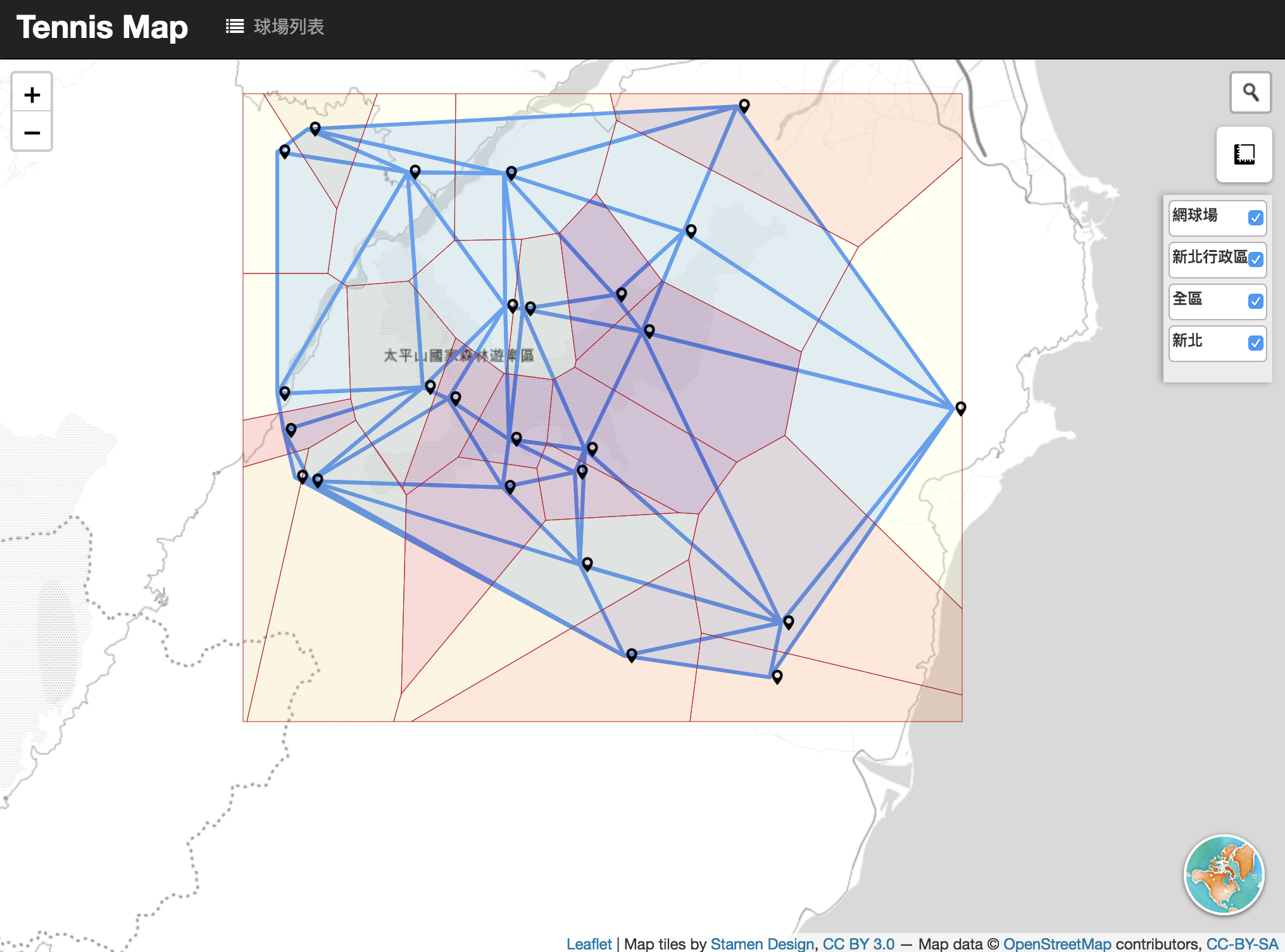

後記

今天介紹了IDW法(規則網格)、TIN(不規則三角網)、Voronoi Diagram，這些方法除了在webGIS會看到，在D3.js等視覺化領域也是很常用到，在turf.js中使用這些方法很簡單，但我自己認為關鍵在於使用時機，要知道每種方法的意義及限制，才不會誤用或誤解算出來的東西，讓資訊傳達更正確。

另外，GIS領域有很多其他更多內插方法，例如Bilinear, Kriging, nearest neighbor等等，這些東西目前turf.js還沒看到，但也可以自己找工具或是自己動手實作看看喔。

今天的程式碼一樣放在github(day19的commit)。

2018鐵人賽-30天打造我的WebGIS系列 web GIS leaflet Turf.js
prev： next：